Fungsi Logaritma adalah | Pengertian dan Definisi

Pengertian dan Definisi fungsi Logaritma. Fungsi Logaritma adalah suatu fungsi yang didefinisikan oleh y = f(x) = alog x dengan a bilangan real, a > 0, a ≠ 1 serta x > 0. x adalah variabel (peubah bebas) dan a adalah bilangan pokok atau basis. Bentuk perpangkatan dalam bentuk logaritma, secara umum adalah sebagai berikut : Jika ab = c dengan a > 0 dan a ≠ 1 maka alog c = b dalam hal ini a disebut basis atau pokok logaritma dan c merupakan bilangan yang dilogaritmakan.

Jika fungsi eksponen menyatakan fungsinya sebagai y=ax, maka fungsi logaritma mempunyai bentuk ylog a=x.  Fungsi Logaritma adalah fungsi yang peubah bebasnya berupa bentuk logaritma. Fungsi Logaritma adalah invers dari fungsi eksponen.

Contoh:

Tulislah bentuk logaritma dari:
a. 2⁵ = 32 maka ²log 32 = 5
b. 4³ = 64 maka ⁴log 64 = 3
c. 2^–2 =1/4 maka ²log 1/4 = –2

Karena fungsi Logaritma adalah fungsiInver dari fungsi eksponensial, maka dari bentuk logaritma di atas, jika ingin di rubah mnejadi fungsi eksponensia, hanya tingal di balik saja. yaitu sebagai berikut:

a.  ²log 32 = 5 maka 2⁵ = 32 

b.  ⁴log 64 = 3 maka 4³ = 64  

c.  ²log 1/4 = –2 maka 2^–2 =1/4 

Definisi Fungsi Logaritma

Misalkan a adalah bilangan positif dengan a ≠ 1. Fungsi logaritma dengan basis a, yang dinotasikan dengan log_a, didefinisikan dengan

log_ax = y    <=>  a ^y= x

 NB: Tanda <=> di baca Jika dan Hanya Jika

Dari definisi di atas dapat di simpulkan, bahwa a log_a x merupakan pangkat dari a untuk menjadi x. 

Dengan cara itu kita bisa menggunakan definisi logaritma untuk mengganti bentuk logaritma log_a x = y menjadi bentuk eksponensial a^y = x, atau sebaliknya, perhatikan bahwa dalam kedua bentuk ini, basisnya tetap sama.

Contoh : Bentuk Logaritma dan Eksponensial

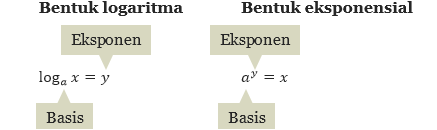
Bentuk logaritma dan eksponensial merupakan persamaan-persamaan yang ekuivalen: Jika bentuk yang satu benar, maka bentuk yang lainnya juga benar. Sehingga kita dapat mengubah bentuk logaritma menjadi bentuk eksponensial, atau sebaliknya, seperti ilustrasi berikut.

Seperti halnya fungsi eksponen, fungsi logaritma juga bisa di gambarkan dalam bentuk grafik. Berikut ini adalah contoh grafik fungsi Logaritma dari f(x)= a ^x

Grafik Fungsi Logaritma dari f(x)= a ^x

Fungsi Logaritma juga memiliki sifat-sifat istimewa. Untuk mengetahui sifat-sifat fungsi Logaritma, bisa anda temukan di Matematika.kamusq.com

Referensi:

• yos3prens.wordpress.com/2015/10/18/fungsi-logaritma-dan-grafiknya/ 
• Wikipedia/fungsilogaritma
• BSE matematika kelas 10
• konsep-matematika/fungsilogaritma